Friday is maths challenge day. Can you solve the problems below?
Challenge 1
Eric bakes these two trays of muffins.
He eats 2 muffins.
His dad eats 3 muffins.
His sister eats 4 muffins.
How many muffins does he have left?
Challenge 2
Lola buys this key ring.
Her mum gives a quarter of the money.
She pays for the rest herself.
How much does she pay herself?
Challenge 3
How old is the teacher?
Challenge 4
Ten trees are planted in a row.
The trees are spaced out equally.
The distance between the fourth and sixth tree is 8 metres.
What is the distance between the first and last tree?
Challenge 5
Filip has these five digit cards.
He uses all of the cards to make a three-digit number and a two-digit number.
He multiplies the two numbers together and the answer is 15,741 .
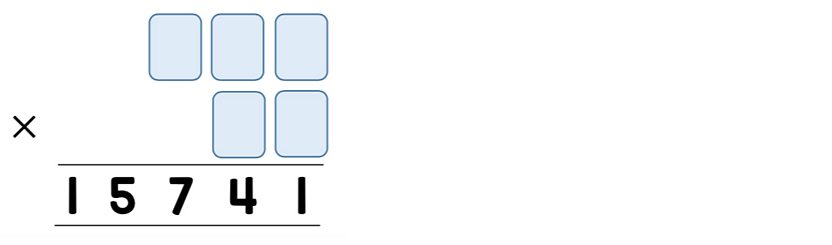
What are the two numbers Filip makes?
Challenge 6
Here are two identical rectangles.
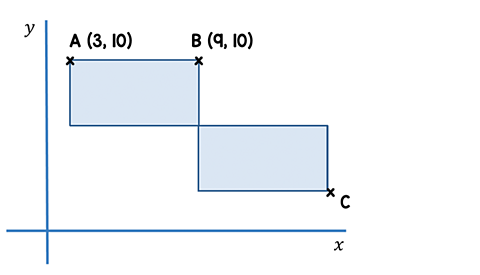
The length of each rectangle is double its width.
Work out the coordinates of point C.
